Définition

\(\triangleright\) Définition de la diffraction

La diffraction est un phénomène dû à la propagation de la lumière qui entraîne des phénomènes visibles remarquables.

Principe d’Huygens-Fresnel

\(\triangleright\) Principe de Huygens-Fresnel

Le principe de Huygens-Fresnel nous dit que la Surface d'onde peut se décomposer en sources secondaires émettant des ondes sphériques. Ces sources secondaires son synchrones, en phase avec l'onde incidente et d'amplitude proportionnelle à cette dernière.
$$A(M)\propto{{\iint A(P)\frac{e^{ikPM} } {PM}d^2\Sigma}}$$

Diffraction de Fresnel

$$A(x,y,z=0)=\iint_{-\infty}^{+\infty}A(x',y',0)\frac{e^{ik\sqrt{D^2+(x-x')^2+(y-y')^2} } }{\sqrt{D^2+(x-x')^2+(y-y')^2} } dx'dy'$$

Approximation paraxiale (petits angles)

On fixe \(D\) et on a les conditions suivantes pour la diffraction de Fresnel:
$$\left(\frac{x-x'}{D}\right)^2\lt \lt 1$$
$$\left(\frac{y-y'}{D}\right)^2\lt \lt 1$$
On prend le premier ordre de développement pour l'exponentielle pour garder la physique. En revanche, au dénominateur, l'approximation à l'ordre \(0\) n'enlève rien.
Alors:
$$A(x,y,D)\approx \iint_{\Sigma} A(x',y',0)\frac{e^{ikD}e^{\frac{ik\left((x-x')^2+(y-y')^2\right)} {2D} } }{D} dx'dy'$$
Avec:

• \(\Sigma\): une surface considérée qui englobe toute la lumière de \(A(x',y',0)\). En dehors, il n'y a pas de lumière.

Remarque: Cette expression n'est valable que si le \(2nd\) ordre est négligeable.
$$kD\left(\frac{y-y'}{D}\right)^4\lt \lt 1$$
$$kD\left(\frac{x-x'}{D}\right)^4\lt \lt 1$$

Diffraction de Fraunhofer

Diffraction "à l'infini"

On considère une source monochromatique qui éclaire une fente de largeur \(a\) à une distance \(D_1\). On observe sur un écran qui est à une distance \(D\to \infty\). (On est toujours dans l'approximation paraxiale)
$$A(x,y,D)\approx \iint_{\Sigma} \underbrace{A(x',y',0)}_{\text{condition initiale} }\frac{e^{ikD}e^{\frac{ik\left((x-x')^2+(y-y')^2\right)} {D} } }{D}$$
$$=\frac{e^{ikD}e^{i\frac{k}{2D}(x^2+y^2) } }{D}\iint_{\Sigma} A(x',y',0)e^{i\frac k{2D}(x'^2+y'^2)}e^{-i\left(\frac{kxx'}{D}+\frac{kyy'}{D}\right)}dx'dy'$$
A \(\Sigma\) fixe, les valeurs \(x'\) et \(y'\) sont fixes:
$$\frac{k(x'^2_{max}+y'^2_{max})}{D}\lt \lt 1$$
On s'intéresse à l'intensité:
$$I=|A(x,y,D)|^2=\frac{1}{D^2}\left|\iint A(x',y',0)e^{-i\left(\frac{kx}{D}x'\right)}e^{-i\left(\frac{ky}{D}y'\right)}dx'dy'\right|^2$$
Le \(\frac{1}{D^2}\) vient du fait qu'à grande distance, l'onde sortant de la fente peut être "considéré" comme une onde sphérique.
L'intensité est proportionnelle au module au carré de la transformée de Fourier de l'onde initiale (ce résultat est vrai pour la diffraction de Fresnel aussi).
On remarque que finalement:
$$I=|A(\alpha,\beta)|^2=\frac{1}{D^2}\left|\iint A(x',y',0)e^{-i\left(\alpha kx'\right)}e^{-i\left(\alpha ky'\right)}dx'dy'\right|^2$$
Avec:

• \(\alpha\): l'angle de projection de \(k\) sur l'axe \(x\)
• \(\beta\): l'angle de projection de \(k\) sur l'axe \(y\)
• \(\Sigma\): une surface considérée qui englobe toute la lumière de \(A(x',y',0)\). En dehors, il n'y a pas de lumière.

Pour une fente de largeur \(a\):
La condition initiale est

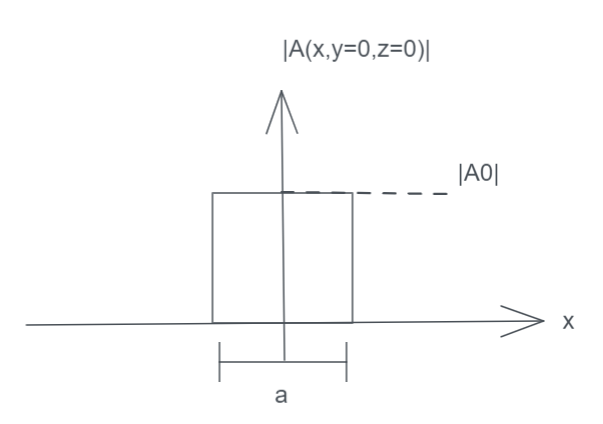
Et l'image sur l'écran est la transformée de Fourier de cette condition initiale, c'est-à-dire une sinus cardinal:
$$I(\alpha_\beta)=(ab)^2|A_0|^2\mathcal{sinc}^2(\frac{\alpha k a}{2})\mathcal{sinc}^2(\frac{\beta k b}{2})$$
La largueur peut être définie, en cherchant les premiers \(\tilde f(\alpha_0)=0\) de la TF :
$$\frac{\alpha_0ka}{2}=\pi$$
$$\alpha_0=\frac{\lambda}{a}$$
Il faut donc que \(a\gt \gt \lambda\)

\(\triangleright\) Définition d'une fente fine

Une fente est dite fine lorsque l'on peut négliger la diffraction d'une direction.
Cette approximation est possible lorsqu'une dimension est très grande devant l'autre.

Translation de l'ouverture dans le plan

Translater la fente dans le plan revient à:
$$TF\left[\Psi(x-x_0)\right]={{TF\left[\Psi(x)\right]e^{-ik_xx_0} }}$$
Cela s'explique par le fait que la distance entre la fente et l'écran est très grande et par conséquent, la figure de diffraction est grande. Un mouvement de la fente sur le plan n'influe que de manière infime sur la position de la figure (le profil d'intensité est identique).

Onde incidente orientée

Si l'on oriente les rayons incidentes (\(A'\)), on trouve:
$$TF\left[A'\right]=TF\left[A\right](k_x=k(\alpha-\alpha_0))$$
Avec:

• \(A\) les rayons incidents normales à la fente

N fentes fines

On a les conditions suivantes:

• $$b\gt \gt a\implies \beta=0$$
• \(\Lambda\gt a\)

$$A(\alpha)=TF\left[A(x)\right](k_x=\alpha k)=\int_{fente 1}A_0e^{-ik_xx}+\int_{fente 2}A_0e^{-ik_xx}+...$$
$$=\text{(diffraction 1 fente)}\left(1+e^{-i\alpha k\Lambda}+e^{i\alpha k2\Lambda}+...+e^{-i(N-1)\alpha k \Lambda}\right)$$
On reconnaît: \(\text{(diffraction 1 fente)}\times \text{(interférence à N ondes)}\)
Finalement:
$$I(\alpha)=I_0\mathcal{sinc}^2\left(\frac{\pi\alpha a}{\lambda}\right)\left[N\frac{\sin(N\alpha\pi\frac{\Lambda}{\lambda} )}{\sin\left(\alpha\pi\frac{\Lambda}{\lambda}\right)}\right]^2$$
$$\alpha_0=\frac{\lambda}{a}$$
$$\alpha=\alpha_{min} =\frac{\lambda}{\Lambda}$$

Réseau de diffraction

Réseau de diffraction

\(\triangleright\) Remarques

Quand on observe dans le plan focal image d'une lentille, c'est équivalent à regarder à l'infini d'après le Théorème de Malus.
Alors, on a:
$$\alpha=\frac{x}{f'}$$
$$\beta=\frac{y}{f'}$$